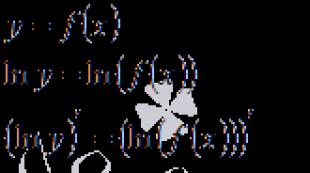Производная лн х. Логарифмическая производная

Производная натурального логарифма от x равна единице, деленной на x:
(1) (ln x)′ = .

Производная логарифма по основанию a равна единице, деленной на переменную x, умноженную на натуральный логарифм от a :
(2) (log a x)′ = .

Доказательство

Пусть есть некоторое положительное число, не равное единице. Рассмотрим функцию, зависящую от переменной x , которая является логарифмом по основанию :
.
Эта функция определена при . Найдем ее производную по переменной x . По определению, производная является следующим пределом:
(3) .

Преобразуем это выражение, чтобы свести его к известным математическим свойствам и правилам. Для этого нам нужно знать следующие факты:
А) Свойства логарифма . Нам понадобятся следующие формулы:
(4) ;
(5) ;
(6) ;
Б) Непрерывность логарифма и свойство пределов для непрерывной функции:
(7) .
Здесь - некоторая функция, у которой существует предел и этот предел положителен.
В) Значение второго замечательного предела:
(8) .

Применяем эти факты к нашему пределу. Сначала преобразуем алгебраическое выражение
.
Для этого применим свойства (4) и (5).

.

Воспользуемся свойством (7) и вторым замечательным пределом (8):
.

И, наконец, применим свойство (6):
.
Логарифм по основанию e называется натуральным логарифмом . Он обозначается так:
.
Тогда ;
.

Тем самым мы получили формулу (2) производной логарифма.

Производная натурального логарифма

Еще раз выпишем формулу производной логарифма по основанию a :
.
Эта формула имеет наиболее простой вид для натурального логарифма, для которого , . Тогда
(1) .

Из-за такой простоты, натуральный логарифм очень широко используется в математическом анализе и в других разделах математики, связанных с дифференциальным исчислением. Логарифмические функции с другими основаниями можно выразить через натуральный логарифм, используя свойство (6):
.

Производную логарифма по основанию можно найти из формулы (1), если вынести постоянную за знак дифференцирования:
.

Другие способы доказательство производной логарифма

Здесь мы предполагаем, что нам известна формула производной экспоненты:
(9) .
Тогда мы можем вывести формулу производной натурального логарифма, учитывая, что логарифм является обратной функцией к экспоненте.

Докажем формулу производной натурального логарифма, применив формулу производной обратной функции :
.
В нашем случае . Обратной функцией к натуральному логарифму является экспонента:
.
Ее производная определяется по формуле (9). Переменные можно обозначить любой буквой. В формуле (9), заменим переменную x на y:
.
Поскольку , то
.
Тогда
.
Формула доказана.

Теперь докажем формулу производной натурального логарифма с помощью правила дифференцирования сложной функции . Поскольку функции и являются обратными друг к другу, то
.
Дифференцируем это уравнение по переменной x :
(10) .
Производная от икса равна единице:
.
Применяем правило дифференцирования сложной функции :
.
Здесь . Подставим в (10):
.
Отсюда
.

Пример

Найти производные от ln 2x, ln 3x и ln nx .

Решение

Исходные функции имеют похожий вид. Поэтому мы найдем производную от функции y = ln nx . Затем подставим n = 2 и n = 3 . И, тем самым, получим формулы для производных от ln 2x и ln 3x .

Итак, ищем производную от функции
y = ln nx .
Представим эту функцию как сложную функцию, состоящую из двух функций:
1) Функции , зависящей от переменной : ;
2) Функции , зависящей от переменной : .
Тогда исходная функция составлена из функций и :
.

Найдем производную от функции по переменной x:
.
Найдем производную от функции по переменной :
.
Применяем формулу производной сложной функции .
.
Здесь мы подставили .

Итак, мы нашли:
(11) .
Мы видим, что производная не зависит от n . Этот результат вполне естественен, если преобразовать исходную функцию, применяя формулу логарифма от произведения:
.
- это постоянная. Ее производная равна нулю. Тогда по правилу дифференцирования суммы имеем:
.

Ответ

; ; .

Производная логарифма модуля x

Найдем производную от еще одной очень важной функции - натурального логарифма от модуля x :
(12) .

Рассмотрим случай . Тогда и функция имеет вид:
.
Ее производная определяется по формуле (1):
.

Теперь рассмотрим случай . Тогда и функция имеет вид:
,
где .
Но производную этой функции мы также нашли в приведенном выше примере. Она не зависит от n и равна
.
Тогда
.

Объединяем эти два случая в одну формулу:
.

Соответственно, для логарифма по основанию a , имеем:
.

Производные высших порядков натурального логарифма

Рассмотрим функцию
.
Мы нашли ее производную первого порядка:
(13) .

Найдем производную второго порядка:
.
Найдем производную третьего порядка:
.
Найдем производную четвертого порядка:
.

Можно заметить, что производная n-го порядка имеет вид:
(14) .
Докажем это методом математической индукции.

Доказательство

Подставим в формулу (14) значение n = 1:
.
Поскольку , то при n = 1 , формула (14) справедлива.

Предположим, что формула (14) выполняется при n = k . Докажем, что из этого следует, что формула справедлива при n = k + 1 .

Действительно, при n = k имеем:
.
Дифференцируем по переменной x :

.
Итак, мы получили:
.
Эта формула совпадает с формулой (14) при n = k + 1 . Таким образом, из предположения, что формула (14) справедлива при n = k следует, что формула (14) справедлива при n = k + 1 .

Поэтому формула (14), для производной n-го порядка, справедлива для любых n .

Производные высших порядков логарифма по основанию a

Чтобы найти производную n-го порядка от логарифма по основанию a , нужно выразить его через натуральный логарифм:
.
Применяя формулу (14), находим n-ю производную:
.

Пусть
(1)
есть дифференцируемая функция от переменной x . В начале мы рассмотрим ее на множестве значений x , для которых y принимает положительные значения: . В дальнейшем мы покажем, что все полученные результаты применимы и для отрицательных значений .

В некоторых случаях, чтобы найти производную функции (1), ее удобно предварительно прологарифмировать
,
а затем вычислить производную. Тогда по правилу дифференцирования сложной функции ,
.
Отсюда
(2) .

Производная от логарифма функции называется логарифмической производной:
.

Логарифмическая производная функции y = f(x) - это производная натурального логарифма этой функции: (ln f(x))′ .

Случай отрицательных значений y

Теперь рассмотрим случай, когда переменная может принимать как положительные, так и отрицательные значения. В этом случае возьмем логарифм от модуля и найдем его производную:
.
Отсюда
(3) .
То есть, в общем случае, нужно найти производную от логарифма модуля функции .

Сравнивая (2) и (3) мы имеем:
.
То есть формальный результат вычисления логарифмической производной не зависит от того, взяли мы по модулю или нет. Поэтому, при вычислении логарифмической производной, мы можем не беспокоится о том, какой знак имеет функция .

Прояснить такую ситуацию можно с помощью комплексных чисел. Пусть, при некоторых значениях x , отрицательна: . Если мы рассматриваем только действительные числа, то функция не определена. Однако, если ввести в рассмотрение комплексные числа, то получим следующее:
.
То есть функции и отличаются на комплексную постоянную :
.
Поскольку производная от постоянной равна нулю, то
.

Свойство логарифмической производной

Из подобного рассмотрения следует, что логарифмическая производная не изменится, если умножить функцию на произвольную постоянную :
.
Действительно, применяя свойства логарифма , формулы производной суммы и производной постоянной , имеем:

.

Применение логарифмической производной

Применять логарифмическую производную удобно в тех случаях, когда исходная функция состоит из произведения степенных или показательных функций. В этом случае операция логарифмирования превращает произведение функций в их сумму. Это упрощает вычисление производной.

Пример 1

Найти производную функции:
.

Решение

Логарифмируем исходную функцию:
.

Дифференцируем по переменной x .
В таблице производных находим:
.
Применяем правило дифференцирования сложной функции .
;
;
;
;
(П1.1) .
Умножим на :

.

Итак, мы нашли логарифмическую производную:
.
Отсюда находим производную исходной функции:
.

Примечание

Если мы хотим использовать только действительные числа, то следует брать логарифм от модуля исходной функции:
.
Тогда
;
.
И мы получили формулу (П1.1). Поэтому результат не изменился.

Ответ

Пример 2

С помощью логарифмической производной, найдите производную функции
.

Решение

Логарифмируем:
(П2.1) .
Дифференцируем по переменной x :
;
;

;
;
;
.

Умножим на :
.
Отсюда мы получаем логарифмическую производную:
.

Производная исходной функции:
.

Примечание

Здесь исходная функция неотрицательная: . Она определена при . Если не предполагать, что логарифм может быть определен для отрицательных значений аргумента, то формулу (П2.1) следует записать так:
.
Поскольку

и
,
то это не повлияет на окончательный результат.

Ответ

Пример 3

Найдите производную
.

Решение

Дифференцирование выполняем с помощью логарифмической производной. Логарифмируем, учитывая что :
(П3.1) .

Дифференцируя, получаем логарифмическую производную.
;
;
;
(П3.2) .

Поскольку , то

.

Примечание

Проделаем вычисления без предположения, что логарифм может быть определен для отрицательных значений аргумента. Для этого возьмем логарифм от модуля исходной функции:
.
Тогда вместо (П3.1) имеем:
;

.
Сравнивая с (П3.2) мы видим, что результат не изменился.

При дифференцировании показательно степенной функции или громоздких дробных выражений удобно пользоваться логарифмической производной. В этой статье мы рассмотрим примеры ее применения с подробными решениями.

Дальнейшее изложение подразумевает умение пользоваться таблицей производных , правилами дифференцирования и знание формулы производной сложной функции .

Вывод формулы логарифмической производной.

Сначала производим логарифмирование по основанию e , упрощаем вид функции, используя свойства логарифма, и далее находим производную неявно заданной функции:

Для примера найдем производную показательно степенной функции x в степени x .

Логарифмирование дает . По свойствам логарифма . Дифференцирование обеих частей равенства приводит к результату:

Ответ: .

Этот же пример можно решить и без использования логарифмической производной. Можно провести некоторые преобразования и перейти от дифференцирования показательно степенной функции к нахождению производной сложной функции:

Пример.

Найти производную функции .

Решение.

В этом примере функция представляет собой дробь и ее производную можно искать с использованием правил дифференцирования. Но в силу громоздкости выражения это потребует множества преобразований. В таких случаях разумнее использовать формулу логарифмической производной . Почему? Вы сейчас поймете.

Найдем сначала . В преобразованиях будем использовать свойства логарифма (логарифм дроби равен разности логарифмов, а логарифм произведения равен сумме логарифмов, и еще степень у выражения под знаком логарифма можно вынести как коэффициент перед логарифмом):

Эти преобразования привели нас к достаточно простому выражению, производная которого легко находится:

Подставляем полученный результат в формулу логарифмической производной и получаем ответ:

Для закрепления материала приведем еще пару примеров без подробных объяснений.

Пример.

Найдите производную показательно степенной функции

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

• Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

• Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
• Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
• Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
• Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

• В случае если необходимо - в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ - раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
• В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности - включая административные, технические и физические - для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.